This is the second article in a series that I started called "Let's talk about computers", in which I aim to document everything that I'm learning about computers. You can find the first article here
Recap
In the previous post I talked about what bits are, how we can convert a binary number to a decimal number and vice-versa and also how we can represent any number between 0 and 255(both included), using 8 bits i.e. using one byte.
Introduction
In this article I'll be talking about how we can perform simple logical operations on bits called Bitwise operations using what are called Logic gates.
Let's establish one important thing before going further. We can think of bit 0 as being equivalent to False or the OFF state and 1 as being equivalent to True or the ON state. I'll talk more about these ON and OFF states later in this post.
Some terms
1) Bitwise operations : The easiest way to think about a bitwise operation is it tests if the relation between two or more given statements is True or False.
2) Operator : A symbol used to specify an operation. For a mathematical operation like addition of two numbers, lets say 2+3, '+' is the operator.
3) Operand : The "thing(s)" on which the operation takes place. For an expression like 2+3, 2 and 3 are the operands. For bitwise logical operations the operands are always bits (0 or 1) since we perform bitwise operations on 0 or 1.
4) Logic gate : A logic gate can be thought of as a device that helps us perform bitwise operations.
Bitwise operations
There are 4 main bitwise operations that we can perform using bits. They are AND, OR, NOT, XOR
Let's talk about them one by one.
AND operation
AND is a bitwise operation that helps us check if BOTH of the given operands are true. If BOTH the given operands are true, it returns true. If even one of them is false, it returns false.
The operator used for AND is ' . ' or ' & '
0 & 0 -> 0 (False AND False returns False)
0 & 1 -> 0 (False AND True returns False)
1 & 0 -> 0 (True AND False returns False)
1 & 1 -> 1 (True AND True returns True)
This can also be represented in the form of a table, called the TRUTH TABLE for the AND operation. Lets represent the first operand as A , second operand as B and the output or the result as C. The truth table is to be read horizontally i.e. for the first row, we can say, if A = 0 and B = 0, then the output C = 0.
| A | B | C |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
One final thing before we move onto the next bitwise operation. AND operation can be performed using a device called an AND Gate. It is represented as follows
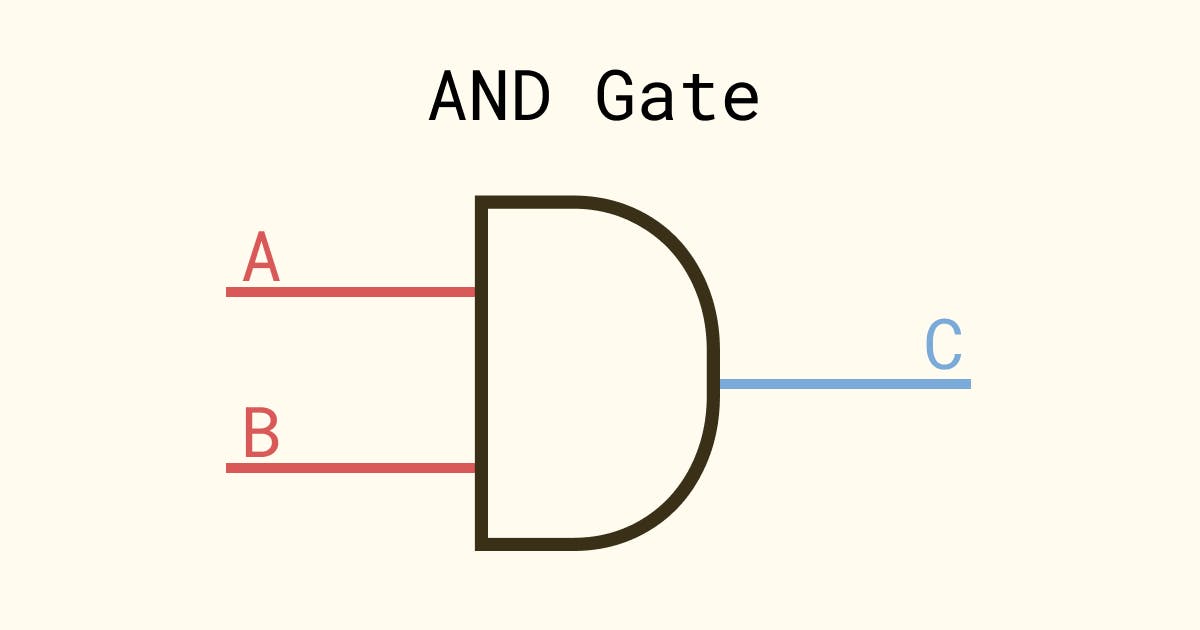
The inputs to this AND Gate are A (first operand) and B (second operand) and the output is C. The inside of such a gate consists of transistors that ensure that the output looks exactly like we saw in the truth table. So for example, if the inputs I give to this AND gate are 0 and 1, the output will become 0.
OR operation
Finally, we are entering into the second bitwise operation. Everything from now on is going to be similar the write up we saw for the AND operation.
OR is a bitwise operation that helps us check if ATLEAST ONE of the given operands is true. So if even one of the operands is true, OR returns TRUE.
The operator used for OR is ' + ' or ' | ' . Therefore, we have
0 | 0 -> 0 (False OR False returns False)
0 | 1 -> 1 (False OR True returns True)
1 | 0 -> 1 (True OR False returns True)
1 | 1 -> 1 (True OR True returns True)
The truth table for the OR operation is :
| A | B | C |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
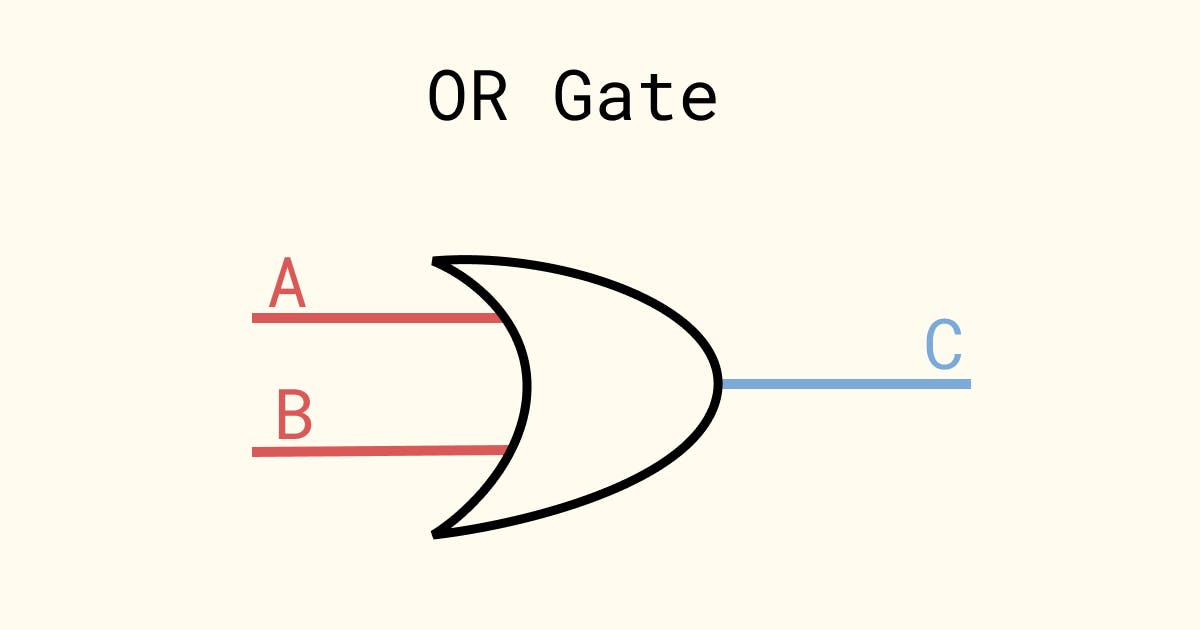
OR operation can be performed using a device called an OR Gate. It is represented as follows.
NOT operation
NOT is a bitwise operation that helps us get the inverse of a given operand. So a TRUE operand returns FALSE and a FALSE operand returns TRUE.
The operator used for NOT is ' ~ ' .
~0 -> 1 (FALSE returns TRUE)
~1 -> 0 (TRUE returns FALSE)
The truth table for the NOT operation is :
| A (Input) | B (Output) |
| 0 | 1 |
| 1 | 0 |
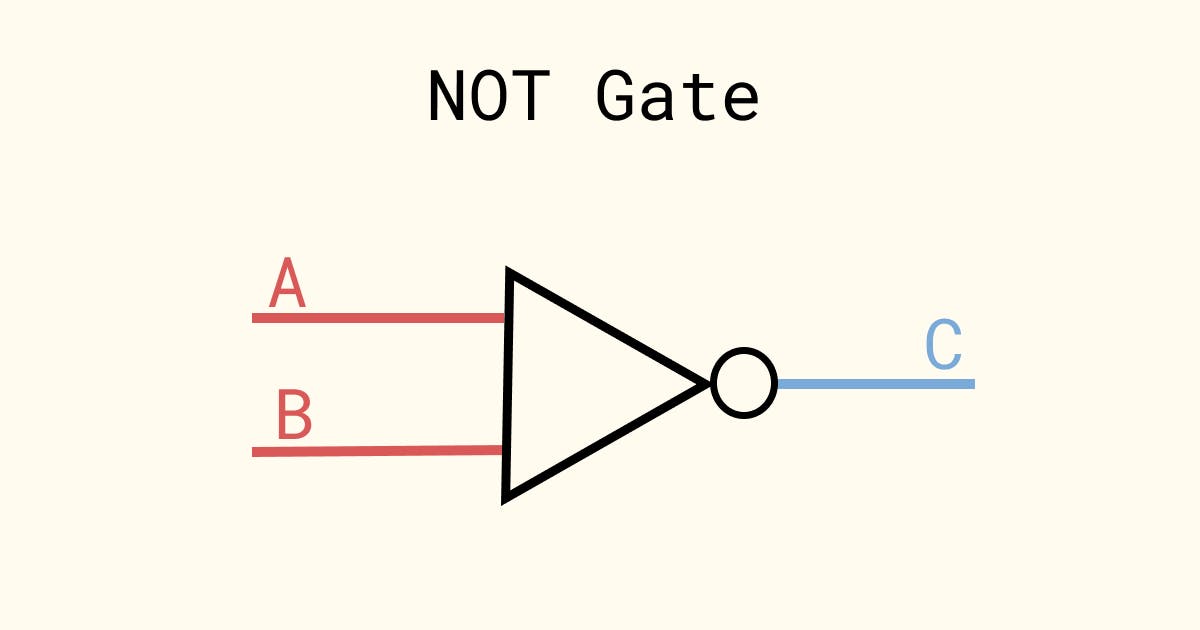
NOT operation can be performed using a device called a NOT Gate. It is represented as follows
XOR operation
XOR or Exclusive OR is a bitwise operation that helps us check if both of the two given operands are equal or not.
If the operands are EQUAL, it returns 0. But if they are not equal, it returns 1.
The operator used for XOR is ' ^ ' .
0 ^ 0 -> 0 (Equal operands so returns 0)
0 ^ 1 -> 1 (Unequal operands so returns 1)
1 ^ 0 -> (Unequal operands so returns 1)
1 ^ 1 -> (Equal operands so returns 0)
The truth table for the XOR operation is :
| A | B | C |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
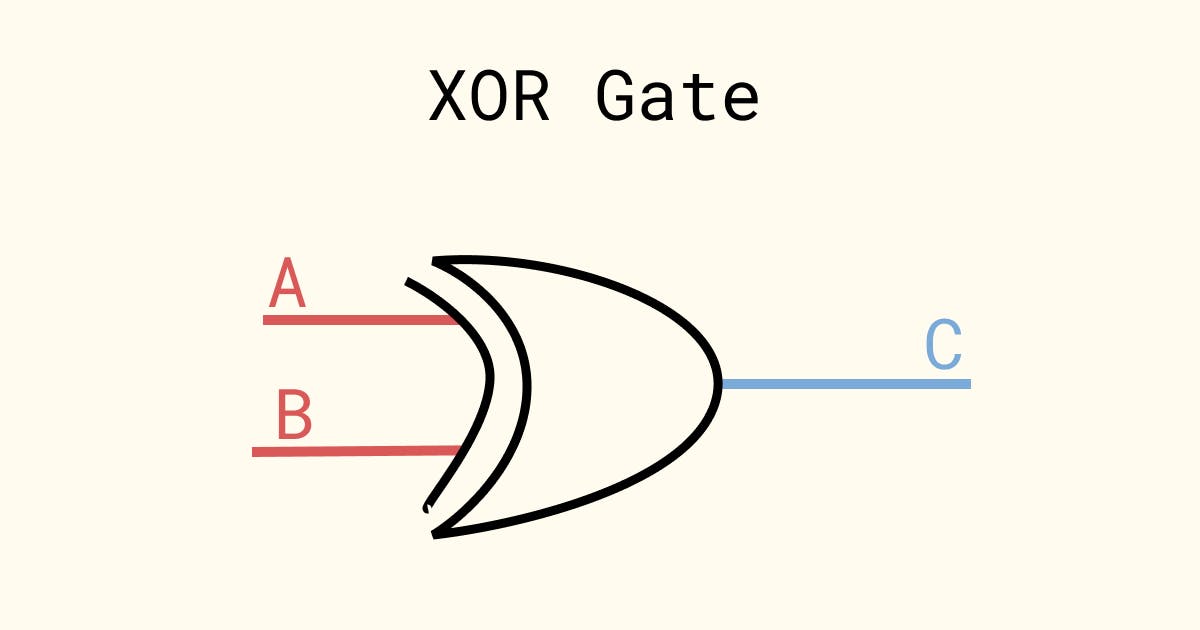
XOR operation can be performed using a device called an XOR Gate. It is represented as follows
All those numbers are fine but what exactly do these logic gates do and how do they identify these bits. Do we type those bits into them as inputs by some mechanism or what exactly happens?
Logic gates are the building blocks of all digital circuits. Any component inside this circuit can persist in any of the following two states.
1) ON state : This is when current flows through the component i.e. there's a flow of current between the component's input and its output.
2) OFF state : This is when current doesn't flow through the component i.e. there's no flow of current between the component's input and its output.
Lets consider one last example to demonstrate how these ON and OFF states (bits 1 and 0) can be thought of as the flow of current.
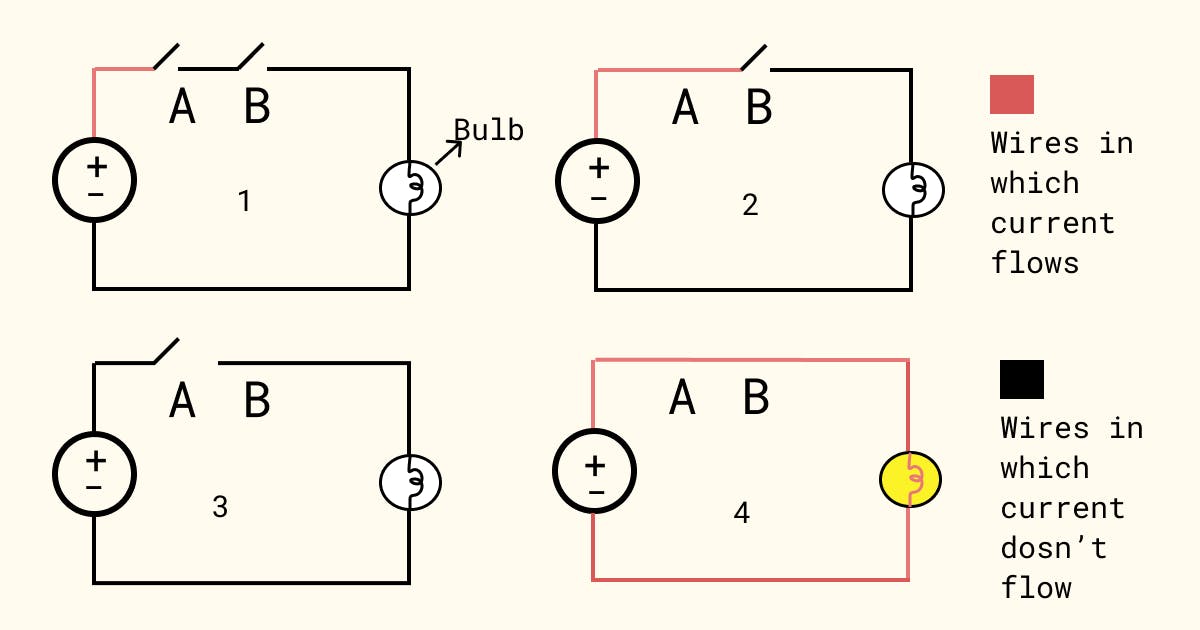
1 : Switches A and B are open
2 : Switch A is closed but B is open
3 : Switch A is open but B is closed
4 : Both switches A and B are closed
In the above circuits, the bulb glows only if the current has a closed path to flow. Lets consider the output as 1 if bulb glows and as 0 if it doesn't glow.
Now if switch A is closed and B is open (case 2), then current flows through A and doesn't flow through B => A=1 and B=0, then the bulb doesn't glow since current doesn't have a closed path to flow. So the output = C = 0.
If A=1 and B=1, i.e. both switches are closed (case 4), the bulb glows since current now has a closed path to flow. So output = C = 1.
If we compare these results to the truth tables we saw before, we can conclude that the above circuit behaves like an AND gate with A and B as inputs and C as output. Therefore, we can consider that the inside of an AND gate has a mechanism like the above circuit going on to ensure that it gives an output of 1 only if both its inputs are 1. Even if one of the inputs is not 1, its output will be 0.
NOTE : The insides of these logic gates don't actually have these bulbs and wires. They are made up of what are called Transistors. These transistors are capable of knowing if current flows through them or not due to the internal chemistry of the material that they are made up of. They behave almost exactly like these bulb-wire circuit equivalents.
Similarly, we can also come up with bulb-wire representations for other gates. Lets look at the OR gate equivalent for now.
OR GATE Equivalent
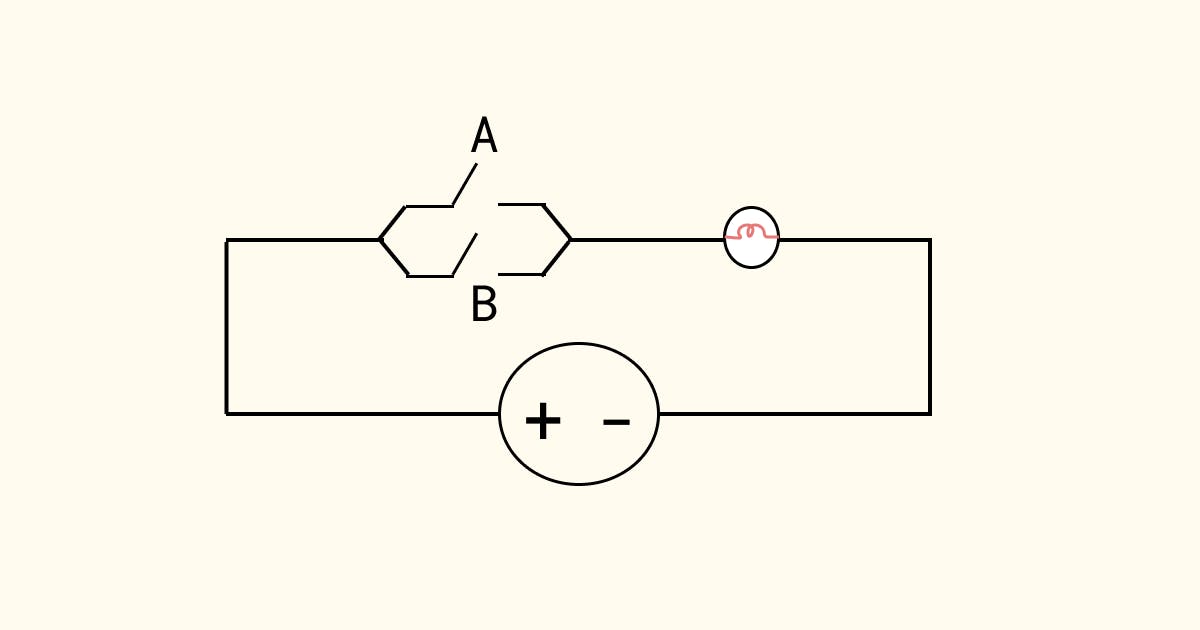
Don't worry if you don't understand how this circuit works. Just remember that all these logic gates can be thought of as simple circuits like these.
Conclusion
In this LONG post, we learnt about
1) Four Bitwise operations : AND, OR, NOT and XOR.
2) We saw what operators are used to represent them i.e. &, |, ~ and ^ respectively.
3) We saw what they physically represent. AND shows us if both the inputs are true, OR shows if atleast one of the inputs is true, NOT gives the inverse of an input and XOR shows if both the inputs are equal or not.
4) We saw how these bitwise operations can be done using logic gates : AND, OR, NOT and XOR gates.
5) At last, we saw how we can think of these gates as being equivalent to circuits made of bulbs and wires.
Next steps
In the next article, I'll show you how these simple gates are used to make some basic components of digital circuits.
